Dans la section sur les comparaisons de fractions, nous avons appris diverses manières de comparer des fractions. La technique de "la croix" peut cependant nous donner à réfléchir.

Par exemple, que se passe-t-il si, avec cette méthode, nous voulons comparer les fractions $fractionsegales 001$ et $fractionsegales 002$ ?

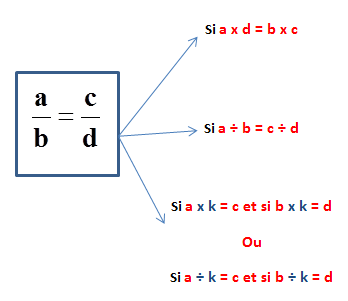
Les deux produits en croix nous donnerons 5 x 6 et 2 x 15 qui font 30.

Autrement dit, aucune fraction n'est plus grande que l'autre. Elles sont donc égales : $fractionsegales 001$ = $fractionsegales 002$ .

2ème partie - Mais qu'est-ce que cela signifie exactement quand on parle de fractions égales ?

a) Regardons ce que cela donne avec deux petits dessins de mêmes dimensions :

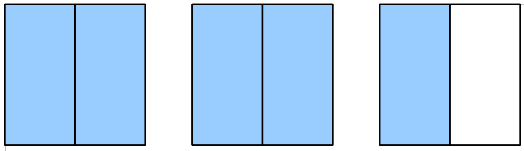La fraction $fractionsegales 001$ pourrait être représentée par : $fractionsegales 003$ .

La fraction $fractionsegales 002$ pourrait être représentée par : $fractionsegales 004$ .

Nous pouvons constater que ces deux illustrations sont identiques : dans chacune d'elle, la même surface a été coloriée.

Autrement dit, deux fractions égales peuvent être représentées par deux dessins de mêmes dimensions,

dans lesquels la même proportion de surface a été coloriée.

b) Regardons ce que cela donne du point de vue du calcul :

La fraction $fractionsegales 001$ correspond à la division de 5par 2. Son quotient exact est 2,5.

La fraction $fractionsegales 002$ correspond à la division de 15par 6. Son quotient exact est aussi de 2,5.

Autrement dit, deux fractions égales représentent des quotients égaux.

c) Regardons les calculs de plus près encore :

Plaçons ces deux fractions côte à côte : $fractionsegales 001$ $fractionsegales 002$ .

Nous pouvons remarquer qu'au niveau des numérateurs, 15 est un multiple de 5 et que 5 x 3 = 15 :

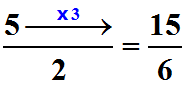
$fractionsegales 005$

De même, nous pouvons remarquer qu'au niveau des dénominateurs, 6 est aussi un multiple de 2 et que, curieusement, 2 x 3 = 6 :

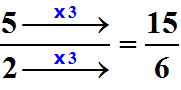
$fractionsegales 006$

Nous pourrions faire le même genre de constat mais avec des divisions si nous voulions passer de $fractionsegales 002$ à $fractionsegales 001$ :

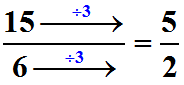
$fractionsegales 007$

Autrement dit, quand nous pouvons passer d'une fraction à une autre en multipliant/divisant le numérateur et le dénominateur par le même nombre, nous pouvons affirmer que ces deux fractions sont égales.

Bilan général :

$fractionsegales 008$

3ème partie - La proportionnalité

Par définition, nous pouvons admettre que deux grandeurs sont proportionnelles l'une à l'autre si la modification de l'une d'elle (par une multiplication ou une division) entraine la modification de l'autre (avec la même opération).

Par exemples :

a) Un gateau pour 6 personnes nécessite 150g de farine. Quelle quantité de farine faudra-t-il pour obtenir un gateau similaire, mais pour 9 personnes ?

Dans ce cas, les deux grandeurs sont "le nombre de personnes" et "la quantité de farine". Nous voyons que la quantité de farine dépend du nombre de personnes. Donc il s'agit d'une situation de proportionnalité.

b) Un enfant pèse 30 kg à 8 ans. Combien pèsera-t-il à 20 ans ?

Ici, les deux grandeurs sont "la masse" et "l'âge". Nous pourrions penser qu'il s'agit d'une situation de proportionnalité, mais si cela en était une, cela voudrait dire par exemple qu'à 16 ans (8 x 2), l'enfant pèserait 60 kg (30 x 2) . En continuant le même raisonnement, cela signifierait qu'à 80 ans (8 x 10), l'enfant pèserait 300 kg (30 x 10). Ce serait assurément absurde. On peut en conclure que cela n'est pas une situation de proportionnalité.

c) Sur une carte routière à l'échelle 1/25000, 10 cm séparent deux villes. Quelle est la distance réelle entre ces deux villes ?

Dans ce cas, les deux grandeurs sont "les dimensions réélles" et "les dimensions sur la carte". Il faut savoir que l'intérêt d'une carte est de donner une représentation fidèle de la réalité, mais en plus petit. La structure générale de la réalité est préservée, mais les dimensions rélles ont été toutes réduites de la même manière, sans qu'il y ait de déformation. Il s'agit donc d'une situation de proportionnalité.

d) Un article coûte 15€. Son prix augmente de 30%. De combien le prix a-t-il augmenté ?

Dans ce cas, les deux grandeurs sont "le prix" et "l'augmentation". Le fait qu'il y ait un "pourcentage" d'augmentation implique une situation de proportionnalité car les pourcentages ont été spécialement créés pour ramener à 100 une situation afin de la rendre plus facilement compréhensible. Donc il s'agit d'une situation de proportionnalité.

4ème partie - Que faire devant un problème décrivant une situation de proportionnalité

La méthode décrite ici peut être appliquée à tous les problèmes relevant d'une situation de proportionnalité : problèmes de recettes, de pourcentage, d'échelles, de trigonométrie, de théorème de Thalès, etc. Tous ces problèmes sont étudiés durant les quatre années du collège.

1ère étape : Lire attentivement le problème afin d'y déceler les deux grandeurs liées l'une à l'autre.

Exemple de problème : Une pompe déverse régulièrement 25 L en 15 secondes. Combien de temps mettra-t-elle pour remplir un bassin de 300 L en conservant toujours le débit indiqué ?

Ici, les deux grandeurs sont "les litres versés" et "le temps mis pour les verser".

2ème étape : Construire un tableau à deux lignes et plusieurs colonnes. Dans la 1ère colonne, indiquer les noms des deux grandeurs décelées dans la consigne du problème :

$fractionsegales 009$

3ème étape : Compléter les colonnes du tableau en plaçant des nombres dans les différentes cases en faisant bien attention de placer, dans la même colonne, les nombres liés ensemble.

Par exemple, ici, les 25 L sont liés aux 15 secondes. Donc ces deux nombres doivent être placés dans la même colonne. Par contre, le 300 L n'a rien à voir avec les 15 secondes ni avec les 25 L. Il sera seul dans sa colonne, dans la ligne dédiée aux litres :

$fractionsegales 010$

4ème étape : C'est celle du calcul qui permet de répondre à la question posée. Pour y arriver, il suffit d'avoir en tête les différents cas possibles d'égalités entre fractions et leurs conséquences sur les calculs (voir la partie 2 ci-dessus).

Par exemple, en voyant cela : $fractionsegales 013$ il faut avoir ceci en tête : $fractionsegales 014$ et on peut alors se demander comment passer de 25 à 300 ? :

$fractionsegales 011$

La réponse peut être obtenue en divisant le nombre d'arrivée par le nombre de départ, donc en calculant 300 ÷ 25 ce qui fait 12 :

$fractionsegales 012$

Puis, en vertu de la méthode expliquée à la Partie 2, nous savons qu'en multipliant aussi 15 par 12 nous trouverons le temps mis pour verser les 300 L : 15 x 12 = 180.

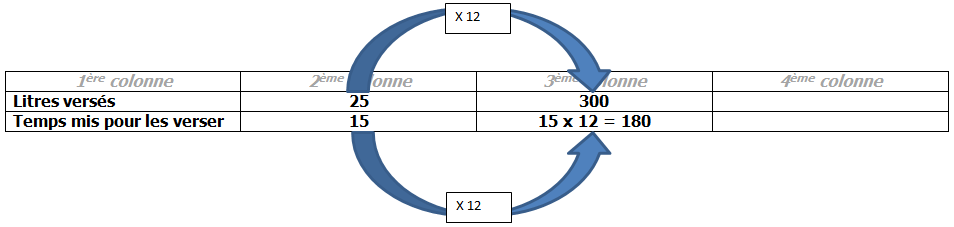
$fractionsegales 015$

Il faut donc 180 secondes (c'est à dire 3 minutes) pour verser 300 L.

5ème partie 5 - Une petite astuce de calcul bien utile

Dans la situation suivante :

$fractionsegales 010$

| Mention légale |