Chiffres et Nombres

Si c'est votre 1ère visite sur cette page, lisez l'article ci-dessous.

Une fois les explications lues, lancez d'abord le QCM se trouvant à la fin de l'article afin de vous tester, puis, après avoir consulter vos résultats, revenez sur cette page, et cliquez sur la palette de chiffres située à droite de cet article. Cela vous permettra de lancer l'atelier d'entraînement →

Rappels sur les différents principes de notre numération

1. Le principe d’addition

A l’origine,ce principe consistait à écrire autant de fois un symbole afin d’arriver au nombre souhaité.

Par exemple, quand les Sumériens (4000 av J.C.) voulaient écrire le nombre « 5 », ils écrivaient cinq fois le symbole correspondant à « 1 », soit :

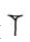
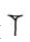
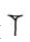
Plus tard, les Egyptiens et les Romains reprirent le même principe dans leurs systèmes de numérations respectifs.

Notre système de numération utilise aussi ce principe, bien que d’une manière légèrement différente car nous y avons joint le principe de position et la base 10.

En effet, quand nous utilisons le nombre « 92 », nous disons « quatre–vingt douze » qui sous–entend « 80 » auquel on a ajouté « 12 ». Autrement dit, nous avons appris à manier naturellement le fait que 92 soit égal à 80 + 12. La grosse différence, qui fait de notre système un progrès considérable par rapport aux précédents, est que notre façon de parler et de lire ces nombres contient en elle ce principe d’addition.

2. La base 10 et le principe de position

L’expression « base 10 » provient du fait qu’au fil des âges, le découpage en paquets de 10 a été perçu comme étant plus « naturel » que les autres partages ayant existé avant lui (par exemple, le partage en base 60 des sumériens qui nous vaut encore aujourd’hui qu’une heure soit égale à 60 minutes, et une minute à soixante secondes).

Ainsi, la base 10 correspond à un décompte par paquets de 10.

On peut avoir :

– Tranche 1 : 0 paquet de 10,

– Tranche 2 : 1 paquet de 10 (ou un multiple de 10, comme 20, 30, ... jusqu'à   90),

– Tranche 3 : 10 paquets de 10 (ou un multiple de 100),

– Tranche 4 : 10 paquets de 10 paquets de 10 (ou un multiple de 1000),

            – etc.

La « contrainte » de ce système est qu’il est impossible d’avoir plus de neuf « éléments » dans chaque tranche, sous peine de devoir passer à la tranche supérieure.

Ainsi, dans la Tranche 1, on peut avoir 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 éléments. Ensuite, on passe à la Tranche 2 où on peut avoir 1 paquet de 10, ou 2, ou 3, ou 4, ou 5, ou 6, ou 7, ou 8, ou 9 mais pas 10 sinon on passe à la Tranche suivante, etc.

Pour plus de facilité, ces Tranches seront écrites sous la forme de "puissances de 10" :

– La Tranche 1 : 0 paquet de 10 s’écrira 10⁰ (on le lit "10 puissance 0" ou bien "10 exposant 0").

– La Tranche 2 : 1 paquet de 10 s’écrira 10¹.

– La Tranche 3 : 10 paquets de 10 s’écrira 10².

– La Tranche 4 : 10 paquets de 10 paquets de 10 s’écrira 10³.

– etc.

L’utilisation de ces Tranches se fait de la manière suivante :

                        Si on a 4 objets, on écrit 4 x 10⁰.

                        Si on a 52 objets, on écrit 5 x 10¹ + 2 x 10⁰.

                        Si on a 483 objets, on écrit 4 x 10² + 8 x 10¹ + 3 x 10⁰.

            On constate que les puissances de 10 apparaissent, de droite à gauche, dans l’ordre croissant de leur exposant. C’est là que repose le principe de position : chaque puissance de 10 correspond en fait à une colonne d’un tableau « infini » de gauche à droite, ou de droite à gauche.

Chaque colonne ne doit contenir qu’un seul chiffre.

Ainsi, pour 52 (qui s'écrit 5 x 10¹ + 2 x 10⁰ ), on a :

Les colonnes de ce tableau sont liées entre elles par une relation de proportionnalité de coefficient 10. Chaque Tranche multipliée par 10 donne la colonne suivante (à gauche) : 

 C’est pourquoi :

                        10¹ = 10 x10⁰= 10¹ x10⁰ = 10¹⁺⁰

                        10² = 10 x10¹ = 10¹ x10¹ = 10¹⁺¹     (les puissances de 10 s’additionnent)

             10³ = 10 x10² = 10¹ x10²⁼ 10¹⁺²

                        Etc.

Pour plus de facilité, dans la lecture et l’écriture des nombres, ces Tranches » on été rassemblées trois par trois dans ce qu’on a appelé« les Classes » :

Dès qu’un chiffre est placé dans une des colonnes (10⁵, 10⁴, 10³), on entend/dit/écrit le mot « mille » ou « millier(s) ».

Dès qu’un chiffre est placé dans une des colonnes (10⁸, 10⁷, 10⁶), on entend/dit/écrit le mot « million(s) ».

Etc.

Afin de distinguer les colonnes d’une même classe, il a été décidé de donner à chacune un nom particulier : unités, dizaines et centaines.

Ces relations entre les puissances de 10 sont étudiées en 4^ème, mais elles sont d’une importance considérable dans :

• le calcul mental,
• le calcul posé,
• l’estimation d’un résultat par les ordres de grandeurs des nombres qui interagissent ensembles,
• et le contrôle de la vraisemblance des résultats obtenus dans des calculs.

C’est pourquoi il est fortement recommandé aux élèves, très tôt dans leur scolarité, mais aussi tout au long du collège, de décomposer les nombres comme suit :

245 = 2x 100 + 4x 10 + 5x 1

       = 2 centaines, 4 dizaines et 5 unités

       = 200 + 40 + 5

       = 2x 10² + 4x 10¹ + 5x10⁰

Les trois premières décompositions sont généralement revues/refaites en 6^ème, mais ces notions sont souvent négligées, voire oubliées dans la suite de la scolarité, alors qu’elles sont primordiales dans le calcul (posé ou mental) .

3.Que doivent maîtriser les élèves de 6ème ?

 (La suite de cet article n'est accessible qu'aux utilisateurs enregistrés)