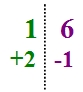Multiplication entre facteurs à deux chiffres

Méthode Générale

Sur notre site, l'expression méthode générale signifiera qu'il s'agit d'une méthode applicable dans tous les cas. Quand une méthode ne sera pas générale, elle sera appelée méthode particulière.

Dans cet article :

• le symbole "/" signifiera une séparation entre deux groupes de chiffres,
• et lorsque deux chiffres seront placés comme ceci 23 le petit chiffre (le 2) de gauche sera une retenue qui sera ajoutée à la colonne située à sa gauche.
  

1ère partie - Rappels élémentaires et multiplication traditionnelle

Selon les tables de multiplication de 1 à 9, à chaque fois que nous effectuons une multiplication entre deux nombres à un chiffre, nous obtenons :

• • • soit un résultat à un chiffre (comme dans 2 x 2 = 4),
    • soit un résultat à deux chiffres (comme dans 2 x 5 = 10).

Par conséquent, lorsque nous multiplierons deux chiffres des unités ensemble, nous obtiendrons :

• • • soit un résultat à un chiffre, c'est à dire des unités,
    • soit un résultat à deux chiffres, c'est à dire des dizaines et des unités.

De la même manière, lorsque nous multiplierons deux chiffres des dizaines ensemble, nous obtiendrons :

• • • soit un résultat à un chiffre, c'est à dire des dizaines,
    • soit un résultat à deux chiffres, c'est à dire des centaines et des dizaines.

Et ainsi de suite avec deux chiffres des milliers, etc.

Par exemple, si nous voulons effectuer 23 x 12, nous écrivons traditionnellement ceci :

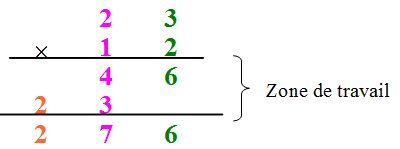
car :

• 2 unités x 3 unités donnent 6 unités,
• 2 unités x 2 dizaines = 4 dizaines,
  
• 1 dizaines x 3 unités = 3 dizaines,
  
• 1 dizaine x 2 dizaines = 2 centaines.
  

Cela explique le décalage dans la zone de travail : il faut que les 4 dizaines soient dans la même colonne que les 3 dizaines afin de rendre leur addition possible.

Cette technique étant apprise en Ecole Elementaire, ne serait-il pas possible, voir nécessaire de s'en affranchir afin d'accélérer les calculs tout en les gérant mentalement ?

La réponse à cette question est "oui" et c'est ce que nous allons voir maintenant.

2ème partie - La méthode "verticalement et en diagonale"

(La suite de cet article n'est accessible qu'aux utilisateurs enregistrés.)

Cette méthode a l'avantage de pouvoir être représentée visuellement par le petit schéma suivant (où chaque point représente un chiffre et où chaque trait rouge symbolise une multiplication entre les points qu'il permet de relier) :

 Par exemple :

Dans le cas de la multiplication précédente 23 x 12, nous aurons :

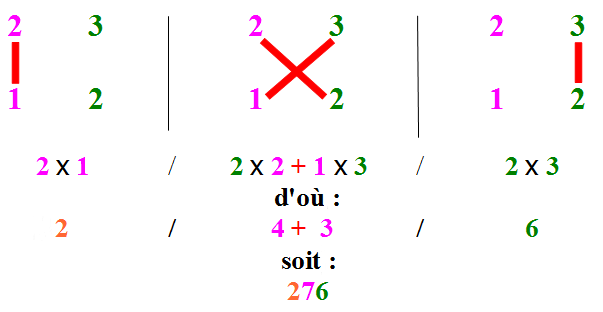
Pour "condenser" encore un peu plus ce "visuel", nous pourrions présenter ce type de multiplication comme ceci :

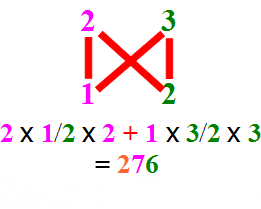
Ou bien, en version abrégée très simple dans les cas où il n'y a pas de retenues (c'est d'ailleurs comme cela qu'elle apparaît lorsqu'on a un peut l'habitude) :

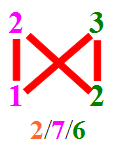
Lors du calcul mental, nous pouvons énoncer le résultat à haute voix et dire "2, 7, 6" ou "6, 7, 2" selon le sens que nous avons choisi pour effectuer le calcul : de gauche à droite ou l'inverse (c'est pourquoi, dans le schéma de la méthode générale, l'étape 1 peut devenir l'étape 3, et inversement). En calcul mental,dire les chiffres les uns après les autres est plus simple que d'essayer de "lire" le nombre en utilisant les mots "cents", "mille", "cent-mille", etc.

3ème partie - La gestion des retenues

Comme nous pouvons nous en douter, les produits peuvent donner des résultats à deux chiffres (et parfois, dans la zone centrale, il peut même y avoir un résultat à trois chiffres), d'où des retenues à gérer. 

Par exemple, dans le produit 23 x 27, nous aurons :

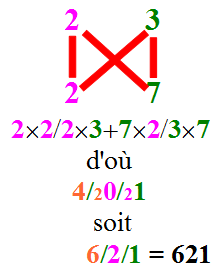
Nous pouvons remarquer qu'en opérant de droite à gauche, il peut être plus facile d'intégrer les retenues au fur et à mesure de la progression des calculs.

4ème partie - Pourquoi passer de la méthode traditionnelle à cette "nouvelle" méthode ?

La première raison, et non la moindre, c'est que cette nouvelle façon de comprendre la multiplication est totalement gérable mentalement, alors que la multiplication traditionnelle ne l'est quasiment pas du tout (trop de choses à gérer, la surcharge cognitive arrive vite, même dans des opérations simples).

Par ailleurs, nous le verrons dans une autre section, cette méthode permet de remarquer des schémas, des similitudes dans certains produits, et alors des méthodes "spéciales" voient le jour, accélérant encore les calculs et leur gestion mentale ! Par exemple, dans le calcul précédent 23 x 27, le résultat peut être obtenu en 3 secondes maximum à partir du moment où l'on sait comment et quoi observer dans une multiplication.

 Les autres avantages de cette méthode sont nombreux :

1. Elle peut être réalisée de gauche à droite, ou de droite à gauche d'où une plus grande flexibilité ;
2. Son caractère très visuel la rend aisé à mémoriser (son côté symétrique par exemple) et plus "dynamique" que la technique traditionnelle, froide et routinière.
3. Nous verrons que ce "visuel" permettra : d'étendre cette technique aux multiplications avec des facteurs très grands, d'expliquer la division comme étant vraiment l'inverse de la multiplication, d'expliquer les opérations entre les fractions, etc.
4. 
   

Bien évidemment, cette nouvelle méthode demande un petit peu d'entrainement afin d'acquérir quelques réflexes de calculs. C'est la raison d'exister de l'Atelier d'Entrainement situé en haut à droite de cet article. N'hésitez pas à vous lancer. Vous ne verrez plus la multiplication comme avant !