Fractions de quelque chose
(Le lecteur est particulièrement invité à tenir compte des couleurs utilisées pendant sa lecture.)
Schéma général
Quel que soit le niveau scolaire, à chaque fois que nous rencontrerons un problème dans lequel il y aura une phrase contenant une expression synonyme de "...une fractiondequelque chose", cela se traduira systématiquement par :
x "quelque chose"
Dans les exemples qui suivent, nous allons rencontrer des situations diverses où ce principe général s'appliquera.
Exemple 1 - La part d'un gateau.
Enoncé du problème :
Un gâteau pèse 350 g. Didier en prend un sixième, Florence prend les deux tiers de ce qui reste, et Romain prend la portion restante.
a) Quelle est la masse de la portion prise par Didier ?
Si nous reprenons l'énoncé en ne regardant que les informations relatives à ce qu'a pris Didier, nous lisons :
"Un gâteau pèse 200 g. Didier en prend un sixième ".
En réalité, l'expression "Didier en prend un sixième " signifie :
"Didier prend un sixième du gateau (de 200 g)"
Donc, conformément au principe général exposé en début de cette page, nous devons effectuer le calcul suivant :
x 200 g
Il reste à savoir comment effectuer ce calcul.
Il y a trois moyens de le mener, et ces trois moyens existeront à chaque fois que nous aurons à calculer "...une fraction de quelque chose". Nous n'aurons qu'à choisir le moyen le plus rapide compte tenu des nombres que nous devons utiliser dans nos calculs.
Moyen n°1 : Nous calculons d'abord le quotient et nous le multiplions par 200 g.
Comme ≈ 0,16 nous avons alors à effectuer 0,16 x 200 g
Nous avons juste à calculer 16 x 2 = 32 g qui est le résultat approché cherché.
Moyen n°2 : Nous calculons d'abord 1x200 g puis nous divisons le produit obtenu par 6.
Comme 1x200 g = 200 g, nous devons calculer 200 g÷ 6 dont le quotient est environ 33 g.
Moyen n°3 : Nous calculons d'abord 200 g÷ 6 puis nous multiplions le quotient obtenu par 1 (c'est sans doute la solution la plus rapide ici). Cela nous donne donc environ 33 g.
b) Quelle est la masse de la portion prise par Florence ?
En reprenant les informations relatives à ce qu'a prix Florence, nous lisons :
"Florence prend les deux tiers de ce qui reste ".
Ici, le sous-entendu est que :
"Florence a pris les deux tiers de ce qui reste après que Didier se soit servi "
Il faut donc calculer ce qui reste après que Didier se soit servi, pour ensuite appliquer un des trois moyens indiqués dans la 1ère réponse à ce problème.
Comme Didier en a pris environ 33 g , il en est resté 200 g - 33 g = 167 g.
Donc "Florence a pris les deux tiers de167 g ".
Maintenant, nous pouvons utiliser le Moyen n°2 :
2 x 167 g = 334 g et 334 g ÷ 3 ≈ 112 g.
c) A quelle fraction du gâteau correspond la portion prise par Romain ?
En reprenant les informations relatives à ce qu'a pris Romain, nous lisons :
"Romain prend la portion restante"
Cela signifie que Romain a pris ce qui restait après que Didier et Florence se soient servis.
Comme Didier en a pris environ 33 g et Florence 112 g, il en reste :
200 g - (33 g + 112 g) = 55 g.
Donc Romain en a pris 55 g.
Comme la question est de savoir la fraction que représente cette quantité par rapport à la quantité de départ, il suffit d'écrire une fraction ayant 55 g comme numérateur, et 200 g comme dénominateur : 
.
Nous pourrions nous arrêter là, mais il est préférable de "simplifier" notre résultat :
Nous avons vu, dans la division décimale à deux chiffres qu'une division était inchangée quand on divisait le dividende et le diviseur par un même nombre.
Ici, voyant que 55 et 200 sont tous les deux des multiples de 5, nous pouvons les diviser par 5 afin de rendre la fraction plus "compréhensible" et surtout écrite avec des nombres plus simples :
55 ÷ 5 = 11 et 200 ÷ 5 = 40.
Donc = 
.
Donc Romain en a pris les "onze quarantièmes".
Exemple 2 - Les pourcentages et leurs utilisation.
Enoncé du problème :
Dans une ville de 37 000 habitants, les élections ont eu lieu. Le candidat du Parti A a récolté 33% des voix, le candidat du Partie B a obtenu 27% des voix, et le candidat du Parti C a eu 37% de ce qui restait. Plusieurs autres candidats ont se sont répartis les voix restantes.
a) Combien de voix a récolté le candidat du Parti A ?
On nous dit :
"Le candidat du Parti A a récolté 33% des voix".
En vertu du principe général expliqué en haut de cette page, nous devons donc calculer 
x 37 000 voix .
Ici, le Moyen n°2 est le plus adapté car on peut remarquer que nous aurons à calculer 33 x 37 qui est une multiplication spéciale.dont le résultat est immédiat :
33 x 37 = 1 221.
Puis 1 221 ÷ 100 donne très vite 12,21.
En réutilisant le "1000" de 37 000 (que nous avions momentanément écarté), nous obtenons donc 12 210 voix pour le candidat du Parti A.
b) Combien de voix a récolté le candidat du Parti B ?
Avec le Moyen n°2, nous aurons à calculer 
x37 000 voix .
27x37 peut se calculer très vite grâce à la méthode générale de la multiplication. Nous obtenons 63549 c'est à dire 999.
Puis en réutilisant le 1000 de 37 000, cela donne 999 000.
Et, enfin, en divisant par 100, nous obtenons 9 990 voix pour le candidat du Parti B.
c) Combien de voix a récolté le candidat du Parti C ?
Le candidat du Parti C a obtenu "37% de ce qui restait".
Comme dans l'Exemple 1 (question c), il est sous-entendu que :
"le candidat du Parti C a obtenu 37% de ce qui restait une fois les voix des candidats A et B enlevées du nombre de voix totales ".
37 000 - (12 210 + 9 990) = 37 000 - 22 200 = 14 800 .
Donc "le candidat du Parti C a obtenu 37% des 14 800 restantes".
Avec le Moyen n°2, nous aurons à calculer 
x 14 800 voix .
(37 x 148 peut se calculer grâce à la méthode traditionnelle. Nous obtenons 5 476.)
Puis en réutilisant les deux zéros de 14 800, cela donne 547 600.
Et enfin, en divisant par 100, nous obtenons 5 476 voix pour le candidat du Parti C.
Exemple 3 - Utilisation d'une échelle sur une carte IGN
Enoncé du problème :
Sur la carte IGN des Calanques de Marseille à Cassis, qui est à l'échelle 1:15 000, on voit l'île de Riou. On sait qu'en réalité elle mesure environ 2,250 km. Combien mesure-t-elle sur cette carte ?
Réponse :
Une carte routière ou une carte IGN est toujours "une représentation de la réalité".
Par conséquent, quand nous lisons :
"...qui est à l'échelle 1:15 000, on voit l'île de Riou. On sait qu'en réalité elle mesure environ 2,250 km"
il faut comprendre :
" le dessin de l'île de Riou représente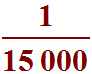 
de 2,250 km"
Nous devons donc calculer :
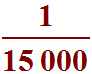x 2,250 km.
Ici, le Moyen n°3 est le plus indiqué : il donne directement 2,250 km ÷ 15 000.
Comme nous mesurons en cm sur notre carte, il faut convertir 2,250 km en cm, ce qui nous donne 225 000 cm.
Nous dvons donc calculer maintenant 225 000 cm ÷ 15 000.
En supprimant les trois zéros de 225 000 et les trois zéros de 15 000, cela revient à calculer 225 ÷ 15 .
Or 225 cm ÷ 15 = 15 cm.
Donc l'ïle de Riou mesure 15 cm sur la carte IGN indiquée.