Division par 11

Dans cette section, nous allons voir comment diviser par 11 aussi facilement que nous pouvons multiplier par 11.

Du fait de la grande ressemblance de cette méthode avec celle de la division par 9, la maitrise de cette dernière est recommandée. De plus, le lecteur est convié à se former aux nombres barrés qui reviennent nous rendre visite pour faciliter certains calculs.

(Au cours de votre lecture, faites bien attention aux couleurs utilisés lors de l'écriture des chiffres. Elles permettent de mieux suivre les explications données.)

1ère partie - Petit aperçu de la méthode ...

Exemple - Nous voulons diviser 239 par 11.

Selon lé méthode de la division par un diviseur à deux chiffres, nous pouvons poser cette division comme suit : 

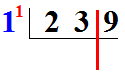
Nous allons systématiquement diviser par 1 et utiliser le 1 dans nos soustractions.

• Dans 2 combien de fois 1 ? Il y a 2 fois et il reste 0. donc : 

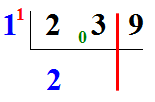
Nous constatons donc que, tout comme dans la division par 9, le 1er chiffre du quotient est le 1er chiffre du dividende !

• 03 - 2 x 1 = 1 et dans 1 combien de fois 1 ? Il y va 1 fois et il reste 0. Donc :
• 
  

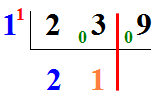
Il semble que nous aurions pu effectuer directement03 - 2 = 1 !

• Et finalement, pour le reste nous faisons 09 - 1 x 1 = 8. D'où :
  

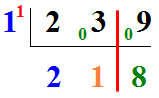
Et il semble bien qu'ici nous aurions pu faire directement09 - 1 = 8 !

En résumé : Il semble que nous aurions pu faire beaucoup plus rapide en suivant les étapes suivantes :

Nous partons de :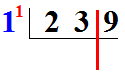 

Nous faisons descendre le 2 du dividende vers le quotient :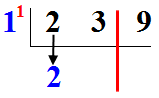 

Puis nous calculons 3 - 2 = 1 :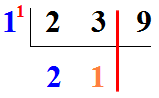 

Et enfin, nous calculons 9 - 1 = 8 :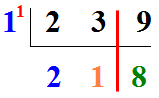 

D'où le résultat final : 239 divisé par 11 donne un quotient de 21 et un reste de 8.

Application de la méthode

Effectuer les divisions suivantes en suivant la méthode expliquée en fin de 1ère partie (juste avec les soustractions :-) )

  Réponses : ici .

2ème partie - Le retour des nombres barrés

Etant donné que nous faisons des soustractions, il se pourrait que nous rencontrions des calculs "impossibles" (comme 3 - 7 par exemple).

Dans ces cas là, nous pouvons user des nombres barrés pour nous tirer d'embarras. En voici un exemple :

"Innover, ce n'est pas avoir une nouvelle idée mais arrêter d'avoir une vieille idée."